数据结构

Trie树

Trie树的定义

Trie树又称字典树，是树形数据结构中的一种，同范畴的还有完全二叉树、红黑树等。

Trie树的检索体现在它使用数据某种公共前缀作为组成树的特点，下面举例说明。

假设有英文组合词taa、tan、tc、in、inn、int，这些词就是我们的数据。分析它们的前缀特点：首先taa、tan、tc这3个单词拥有公共的开头字母t，这就是它们的公共前缀，归为一类；然后in、inn、int的公共开头字母是i，根据这个特点，我们得到如下图所示的树形图。

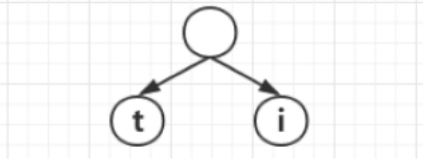
接着继续分析，在taa、tan、tc中标出第一个字母t后，剩下的分别是aa、an、c。可以看到，aa和an拥有公共的前缀字母a，因此模仿上面的前缀规则可以继续完成树形图，如下图所示。

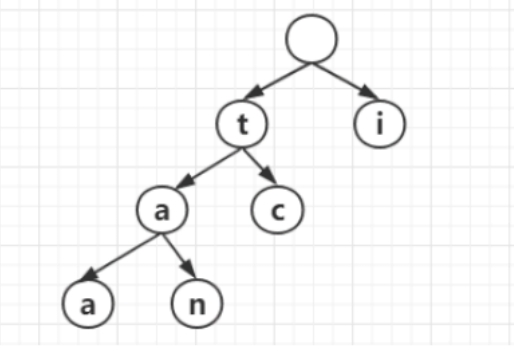
至此，从树项节点开始自上而下看，所走过的节点值连起来就是taa、tan、tc。继续完善前缀i字母的子树，最终整个Tie的前缀树如下图所示。

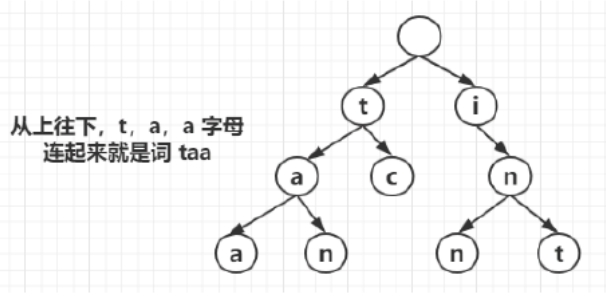
如果例子中在起始的时候多出一个和其他节点没有公共前缀的单词，例如egg，那么树图从顶部开始将分成3个分支，分别是t、i、e，而不是两个。

最终，各个单词被包含在Trie树中。一棵Trie树满足下面的特点：

• 不一定是二叉树。
• 根节点不包含字符，除根节点以外每个节点只包含一个字符，注意是字符不是字符串。
• 从根节点到某一个节点，自上而下，路径上经过的字符连接起来就为目的节点对应的字符串。
• 每个节点的所有子节点包含的字符串不相同。

Trie树的应用

为什么要在软件应用中采用Trie树这种数据结构呢？这是因为Trie树在针对字符串搜索方面有很好的性能。

接着Trie树的例子，如果我们要查找tan这个单词，可以按照下面的步骤来执行。

• 首先自上而下，先查找字母t，如果找到了t，那么不是t的分支就不需要考虑了。
• 接着查找字母a，以此类推。
• 最终找剩下的字母n。

在上述查找过程中，最大限度地减少了无谓字符的比较，但由于Trie树的非根节点存储的是每一个字符，导致Trie树会消耗大量的内存，这也是Trie树的一个缺点。此外，Trie树中由于字符串之间没有公共的字母前缀，因此树的层级也会比较高。

比如说taa和tcn，它们只有t字母是公共的，那么如果是t -> aa和t -> cn就只有两层的高度，而在Tire树中，却被表示为了t -> a-> a和t -> c-> n，拥有3层的高度。

Patricia Trie树

Patricia Trie树也是一种Trie树。不同点在于，它是Trie树的升级版，在Trie树的基础上做了优化：非根节点可以存储字符串，而不再仅仅是字符，节省了空间的花销。

仍然以上一节的Trie树为例，我们画出Patricia Trie树的树形图，单词是taa、tan、tc、in、inn、int，如下图所示。

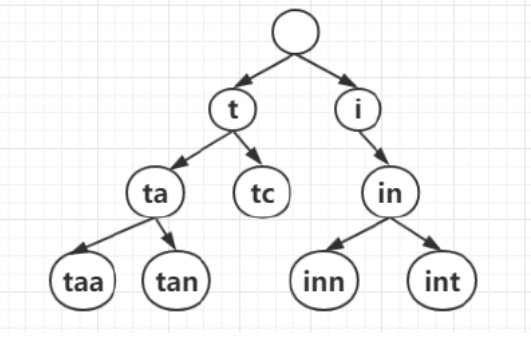
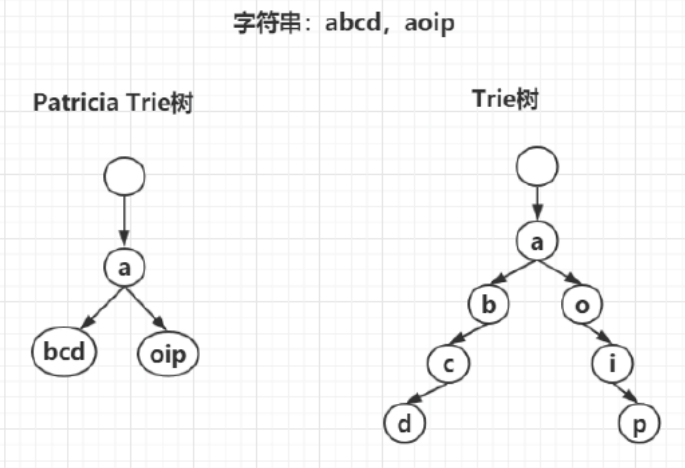
这里我们给出abcd和aoip两个字符串的Patricia Trie树和Trie树的树形图，如下图所示。可以明显地看到，那些很长但又没有公共节点的字符串在Patricia Trie树中占用的空间更少。

默克尔树(Merkle Tree)

默克尔树又被称为哈希树(Hash Tree)，它满足树的数据结构特点，拥有下面的特点，也就是说，默克尔树必须满足下面的条件。

• 树的数据结构，常见的是二叉树，但也可以是多叉树，它具有树结构的全部特点。
• 基础数据不是固定的，节点所存储的数据值是具体的数据值经过哈希运算后所得到的哈希值。
• 哈希的计算是从下往上逐层进行的，就是说每个中间节点根据相邻的两个叶子节点组合计算得出，根节点的哈希值根据其左右孩子节点组合计算得出。
• 最底层的节点包含基础的数据。

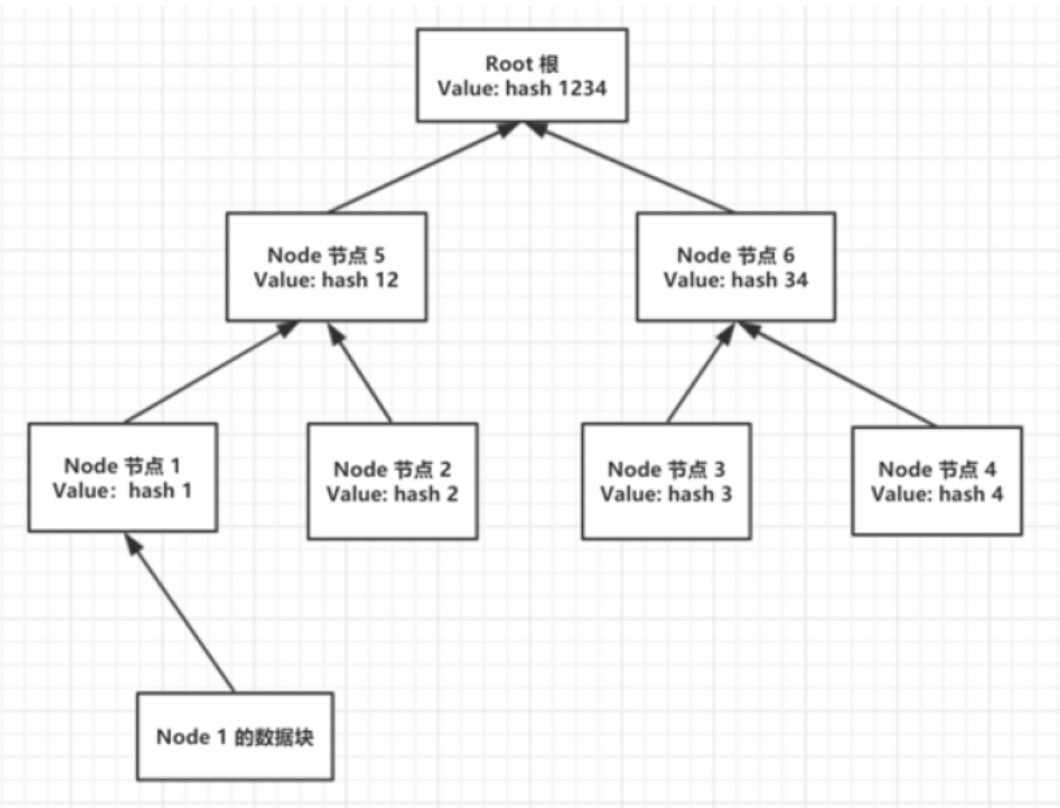
自下而上地看，最底层节点Node节点1的数值Value是hash 1，hash1是由Nodel对应的数据块经过一定的哈希算法生成的，其他的最底层节点也有对应的数据块。此处对应默克尔树的第4个特点。

Node节点5是Node节点1和Node节点2的父亲节点，那么Node节点5的哈希值由Node节点1和Node节点2的哈希值得出。具体父节点的值如何计算，并没有统一的方法，可以定义某一种算法，只要满足父节点的值为其左右叶子节点的值经过一定计算得出即可。图2-32采 用了字符串拼接的计算方式：Value(5)=Value(1)+Value(2)=12。此条对应默克尔树的第3个特点。

由于生成哈希值的原始数据几乎都是字节流，因此底层数据块的内容不会被限制，类似于区块头，拥有多种数据类型，也可以是单独的一个字符串。此条满足默克尔树的第2个特点。

我们从图2-32中可以很直观地看出，该默克尔树就是数据结构中的二叉树模型。

默克尔树的节点插入

上图是一种完全二叉树的形式。在此类二叉树中，当一个新的数据块产生的哈希值形成的新的节点要插入树中时，如果所要被插入的默克尔树底层的节点己经是满叶子的情沉，它会按照如下图所示的形式插入。

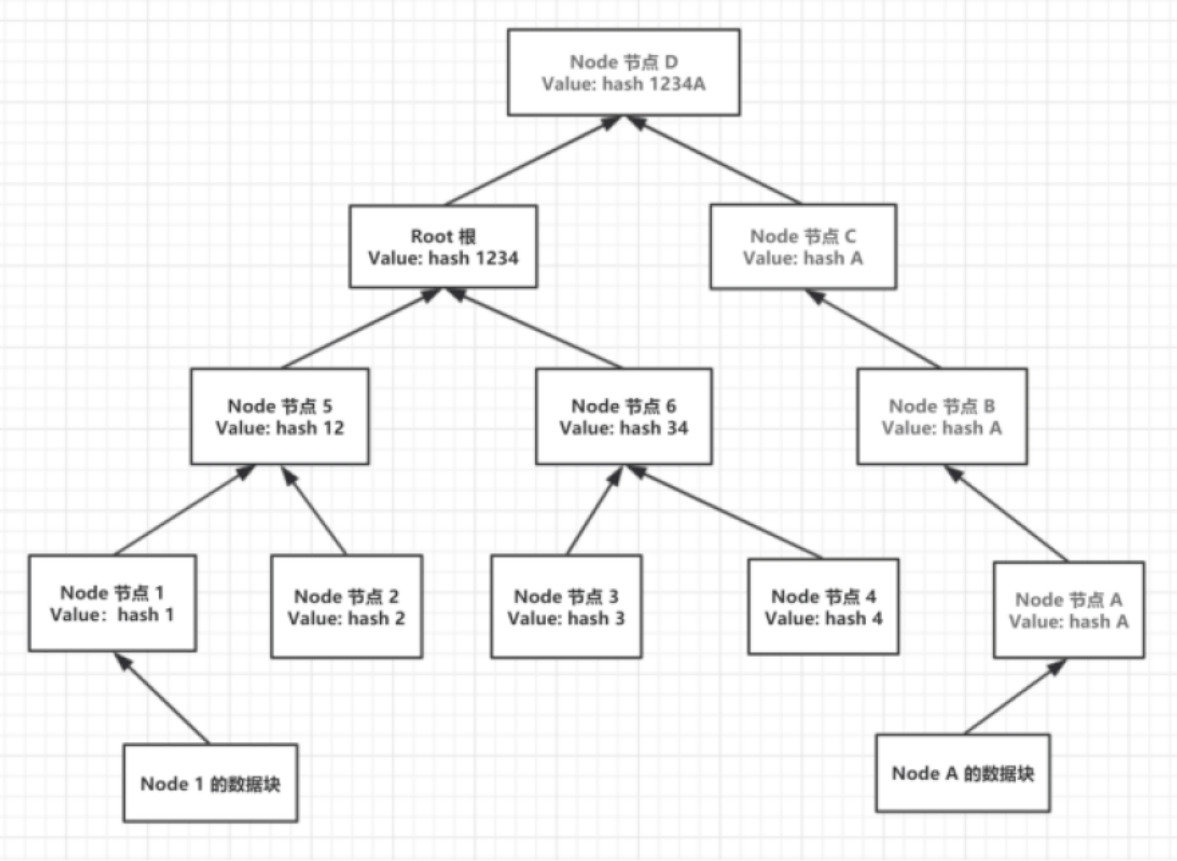
在这种情况下，新插入的叶子节点会自动在不同的层数生成与最底层新插入的节点所拥有相同数值的节点，下图新插入节点为A，据此依次生成B、C、D，最后的D节点是新的根节点(Root)。

至此，我们知道，区块Header内部的Root、TxHash、ReceiptHash这3个值的含义其实都是默克尔树的根，它们所在的树依次对应于：

区块体内的账户(Account)对象数组。在打包交易中该对象数组会时刻被更新。

被打包进当前区块的交易(Transaction)列表数组。该列表数组在所有交易打包完之后生成。

区块内的所有交易(Transaction)完成之后生成的一个Receipt数组。

默克尔树数据验证

默克尔树的作用体现得最多的地方就是它可被用于数据的验证。在以太坊中，默克尔树可以用来验证区块内的交易(Transaction)，因为以太坊的交易是被矿工打包进到区块中的，所以一个区块内部包含有很多笔交易信息。

根据默克尔树父节点的哈希值与其叶节点值的关系，如果当前默克尔树的底层数据块是交易数据，那么往上的节点中，其所包含的哈希值都是由交易数据生成的。

根据节点中哈希值的关联关系，可以对某笔交易数据进行验证，如下图所示。

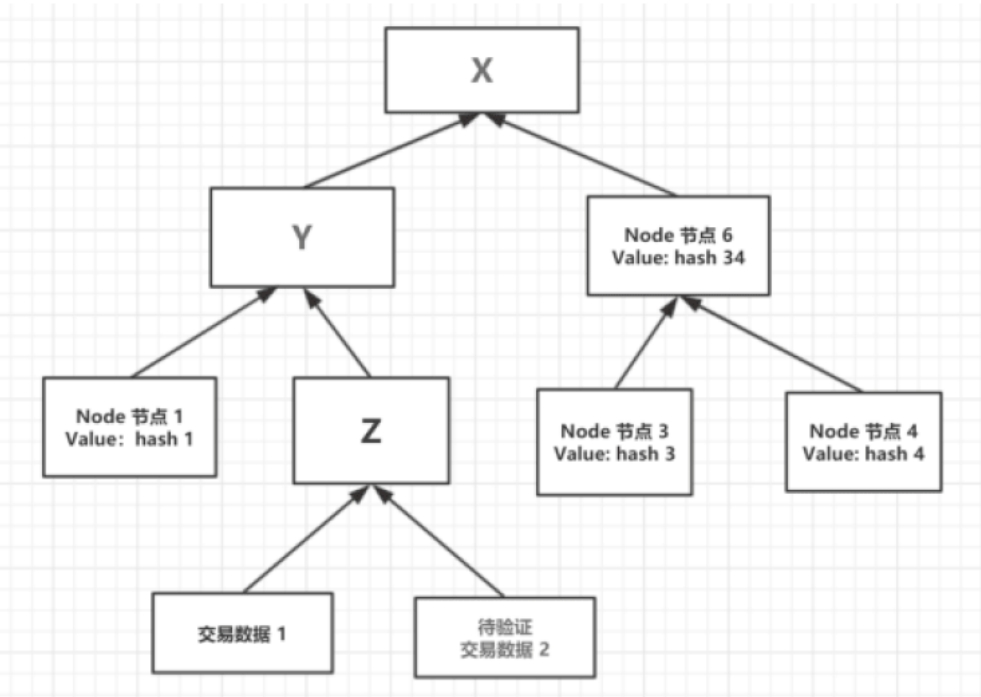
假设我们知道了交易数据1、Node节点1和Node节点6，现在要验证交易数据2是否在当前的默克尔树中。首先由交易数据1和交易数据2生成Z节点的哈希值，然后由Node节点1和Z节点生成Y节点的哈希值，最后由Y节点和Node节点6生成根节点X的哈希值。在得到了根节点X的哈希值之后，再将它和区块头部中的TxHash值进行比较，判断它们是否相等，如果相等，证明交易数据2存在于当前区块的交易列表中，反之则不是。

默克尔树交易数据的验证应用还存在于点对点的视频流中。例如，将一部完整影片的数据流拆分成多个数据块，并由这些数据块组成默克尔树。当用户下载影片时，就能根据节点值来对应下载自己所缺少的那一部分，在数据被损坏的时候也能进行下载修复，而不需要重新下载整部影片。